Quantitative Investment Analysis - Chapter 3
In this post we will solve the end of the chapter practice problems from chapter 3 of the book.
Here are the first 6 problems and their solutions in R

library(tidyverse)Problem 1
B. The FTSE Eurotop 100 as a representation of the European stock market
Problem 2
A. Ordinal
Problem 3
A. The 500 companies in the S&P 500 Index
Problem 4
A. median of a population.
Problem 5
df <- tibble(return_interval = c("-10 to -7", "-7 to -4", "-4 to -1", "-1 to 2", "2 to 5", "5 to 8"),
absolute_freq = c(3,7,10,12,23,5)) %>%
mutate(r_freq = absolute_freq / sum(.$absolute_freq)) %>%
mutate(cum_sum = cumsum(r_freq))
df## # A tibble: 6 x 4
## return_interval absolute_freq r_freq cum_sum
## <chr> <dbl> <dbl> <dbl>
## 1 -10 to -7 3 0.05 0.05
## 2 -7 to -4 7 0.117 0.167
## 3 -4 to -1 10 0.167 0.333
## 4 -1 to 2 12 0.2 0.533
## 5 2 to 5 23 0.383 0.917
## 6 5 to 8 5 0.0833 1A. The relative frequency of the interval “–1.0 to +2.0” is 20%.
Problem 6
tibble(year = 1:12,
returns = c(2.48, -2.59, 9.47, -0.55, -1.69, -0.89, -9.19, -5.11, 1.33, 6.84, 3.04, 4.72)) %>%
group_by(group = cut(returns, breaks = 5)) %>%
#group_by(group = cut(returns, breaks = seq(min(returns), max(returns), length = 5))) %>%
summarise(n = n()) %>%
mutate(rel_freq = n / sum(.$n)) %>%
mutate(c_freq = cumsum(rel_freq))## # A tibble: 5 x 4
## group n rel_freq c_freq
## <fct> <int> <dbl> <dbl>
## 1 (-9.21,-5.46] 1 0.0833 0.0833
## 2 (-5.46,-1.73] 2 0.167 0.25
## 3 (-1.73,2.01] 4 0.333 0.583
## 4 (2.01,5.74] 3 0.25 0.833
## 5 (5.74,9.49] 2 0.167 1C. 0.5833

Problems 7 to 8 problems and their solutions in R
Problem 7
A. tabular display.
Problem 8
(2 + 7 + 15 ) / 26## [1] 0.9230769C. The cumulative relative frequency of Interval C is 92.3%.
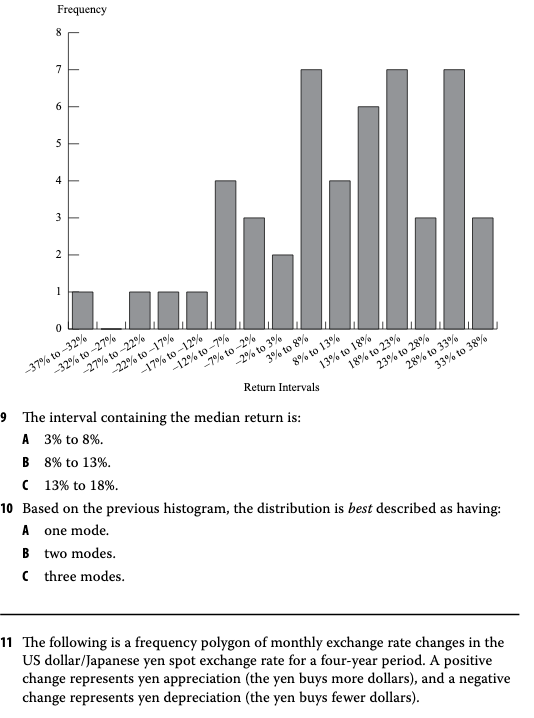
Problems 9 to 10 problems and their solutions in R
Problem 9
C. 13% to 18%
Problem 10
C. three modes
Problems 11 to 12 problems and their solutions in R
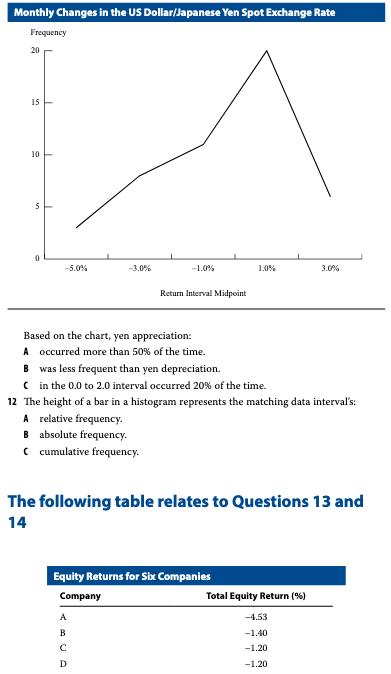
Problem 11
The following is a frequency polygon of monthly exchange rate changes in the US dollar/Japanese yen spot exchange rate for a four-year period. A positive change represents yen appreciation (the yen buys more dollars), and a negative change represents yen depreciation (the yen buys fewer dollars). (See chart above)
Based on the chart, yen appreciation: - A. occurred more than 50% of the time. - B. was less frequent than yen depreciation. - C. in the 0.0 to 2.0 interval occurred 20% of the time.
A. occurred more than 50% of the time.
Problem 12
B. absolute frequency.
Problems 13 to 16 problems and their solutions in R
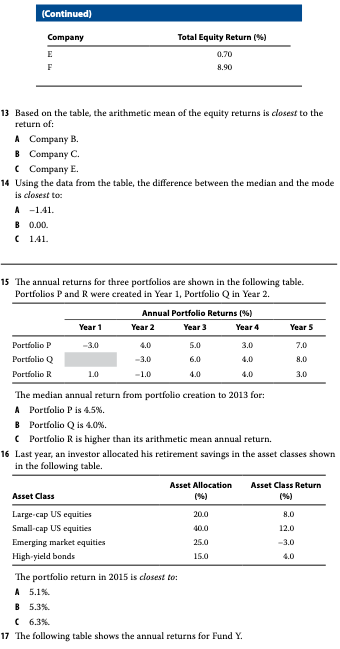
Problem 13
df <- tibble(company = c("A", "B", "C", "D", "E", "F"),
eq_ret = c(-4.53, -1.40, -1.2, -1.2, 0.7, 8.9))
df## # A tibble: 6 x 2
## company eq_ret
## <chr> <dbl>
## 1 A -4.53
## 2 B -1.4
## 3 C -1.2
## 4 D -1.2
## 5 E 0.7
## 6 F 8.9mean(df$eq_ret)## [1] 0.2116667C. Company E
Problem 14
# Median
med <- median(df$eq_ret)
# Mode is most freq value -1.2
mod <- -1.2
med - mod## [1] 0B. 0
Problem 15
C. Portfolio R is higher than its arithmetic mean annual return.
Problem 16
20.08.0Small- cap US equities40.012.0Emerging market equities25.0–3.0High- yield bonds15.04.0
df <- tibble(asset_class = c("Large - cap US equities", "Small - cap US equities",
"Emerging market equities", "High yield bonds"),
allocation = c(20,40,25,15),
returns = c(8,12,-3,4))
df %>%
mutate(allocation = allocation / 100) %>%
mutate(contribution = allocation * returns) %>%
summarise(port_ret = sum(contribution))## # A tibble: 1 x 1
## port_ret
## <dbl>
## 1 6.25C. 6.3%
Problems 17 to 20 problems and their solutions in R

Problem 17
df <- tibble(year = 1:5,
returns = c(19.5, -1.9, 19.7, 35, 5.7))
df %>%
mutate(returns = returns/100) %>%
mutate(r = 1 + returns) %>%
mutate(cr = cumprod(r)) %>%
select(cr) %>%
slice(n()) %>%
.[[1]]## [1] 2.0023492.002349 ** (1/5) - 1## [1] 0.1489681A. 14.9%
Problem 18
df <- tibble(year = 1:4,
price = c(62,76,84,90))
df %>%
mutate(shares = 5000 / price) %>%
summarise(s = sum(shares)) %>%
.[[1]]## [1] 261.51420000 / 261.514## [1] 76.47774A. $76.48
Problem 19
df <- tibble(year = 1:10,
returns = c(15.25, 10.02, 20.65, 9.57, -40.33, 30.79, 12.34, -5.02, 16.54, 27.37))
quantile(df$returns, 0.8, type = 6)## 80%
## 26.026A. 26.03%
Problem 20
df <- tibble(year = 1:10,
returns = c(15.25, 10.02, 20.65, 9.57, -40.33, 30.79, 12.34, -5.02, 16.54, 27.37))
mean_ret <- df %>%
filter(year >= 6) %>%
summarise(m = mean(returns)) %>%
.[[1]]
df %>%
filter(year >= 6) %>%
mutate(m = abs(returns - mean_ret)) %>%
summarise(mm = mean(m))## # A tibble: 1 x 1
## mm
## <dbl>
## 1 10.2A. 10.20 %
Problems 21 to 22 problems and their solutions in R
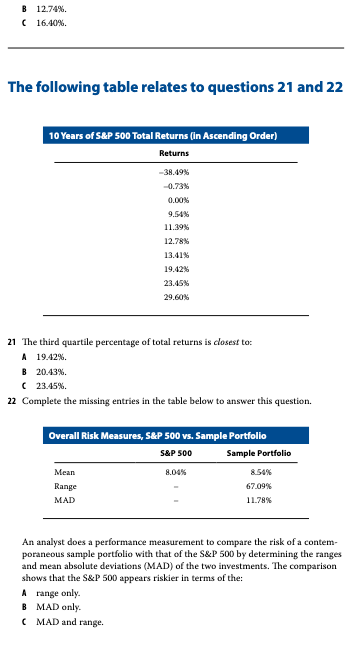
Problem 21
df <- tibble(returns = c(-38.49, -0.73, 0.00, 9.54, 11.39, 12.78, 13.41, 19.42, 23.45, 29.60))
df## # A tibble: 10 x 1
## returns
## <dbl>
## 1 -38.5
## 2 -0.73
## 3 0
## 4 9.54
## 5 11.4
## 6 12.8
## 7 13.4
## 8 19.4
## 9 23.4
## 10 29.6quantile(df$returns, type = 6)## 0% 25% 50% 75% 100%
## -38.4900 -0.1825 12.0850 20.4275 29.6000B. 20.44%
Problem 22
sp_range <- abs(min(df$returns) - max(df$returns))
sp_mad <- mad(df$returns, center = mean(df$returns))
sp_range## [1] 68.09sp_mad## [1] 12.45681C. MAD and range
Problems 23 to 26 problems and their solutions in R
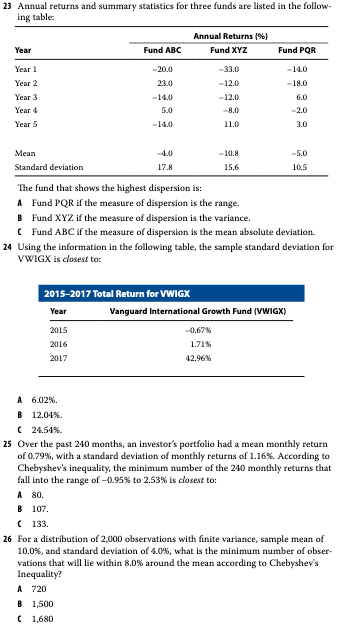
Problem 23
abc <- c(-20,23,-14,5,-14)
xyz <- c(-33,-12,-12,-8,11)
pqr <- c(-14,-18,6,-2,3)
get_stats <- function(x,y) {
r <- abs(min(x) - max(x))
v <- var(x)
m <- mad(x, center = mean(x))
cat(r,v,m,"for",y)
}
get_stats(abc,'abc')## 43 316.5 14.826 for abcget_stats(xyz,'xyz')## 44 244.7 4.15128 for xyzget_stats(pqr,'pqr')## 24 111 13.3434 for pqrC. Fund ABC if the measure of dispersion is the mean absolute deviation.
Problem 24
ret <- c(-0.67, 1.71, 42.96)
sd(ret)## [1] 24.53163C. 24.54
Problem 25
mean_ret <- 0.79
sd_ret <- 1.16
upper_limit <- 2.53 - mean_ret
lower_limit <- -0.95 - mean_ret
k <- upper_limit / sd_ret
(1 - 1/k^2) * 240## [1] 133.3333C. 133
Problem 26
k <- 8/4
(1 - 1/k^2) * 2000## [1] 1500B. 1500
Problems 27 to 35 problems and their solutions in R
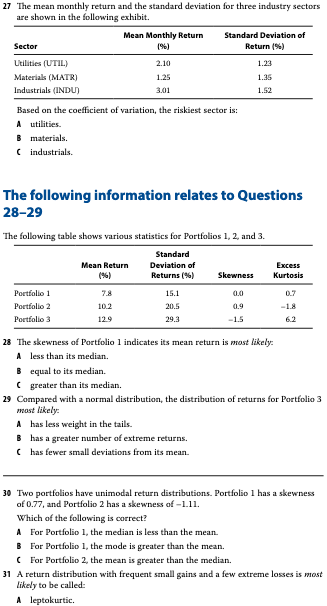

Problem 27
df <- tibble(sector = c("utilities", "materials", "industrials"),
mean_ret = c(2.1, 1.25, 3.01),
sd_ret = c(1.23, 1.35, 1.52))
df %>%
mutate(v = sd_ret / mean_ret)## # A tibble: 3 x 4
## sector mean_ret sd_ret v
## <chr> <dbl> <dbl> <dbl>
## 1 utilities 2.1 1.23 0.586
## 2 materials 1.25 1.35 1.08
## 3 industrials 3.01 1.52 0.505B. matrials
Problem 28
B. equal to its median.
Problem 29
B. has a greater number of extreme returns
Problem 30
A. For Portfolio 1, the median is less than the mean.
Problem 31
C. negatively skewed.
Problem 32
B. mode < median < mean
Problem 33
B. platykurtic
Problem 34
B. The geometric mean measures an investment’s compound rate of growth over multiple periods.
Problem 35
B. Geometric